要約
アンカー付き長方形配置問題の遺伝的アルゴリズムによる解法を行った。
問題設定
入力
平面上の $(0, 0)$ と $(1, 1)$ の正方形の領域内の点群 $P$ を入力。
- 頂点数: $n = |P|$
- $(x_i, y_i)\in P$
- $x_i \ne x_j \land y_i \ne y_j \quad (i\ne j)$
- $(0, 0)\in P$
出力
互いに重ならない $n$ 個の長方形 $R$ を出力。
- $r_i\in R$ の左下座標は $(x_i, y_i)$
- $r_i\in R$ の右上座標は $(x_i^\prime, y_i^\prime)$ で、$x_i < x_i^\prime$ かつ $y_i < y_i^\prime$
各長方形の左下の頂点が入力点群である。
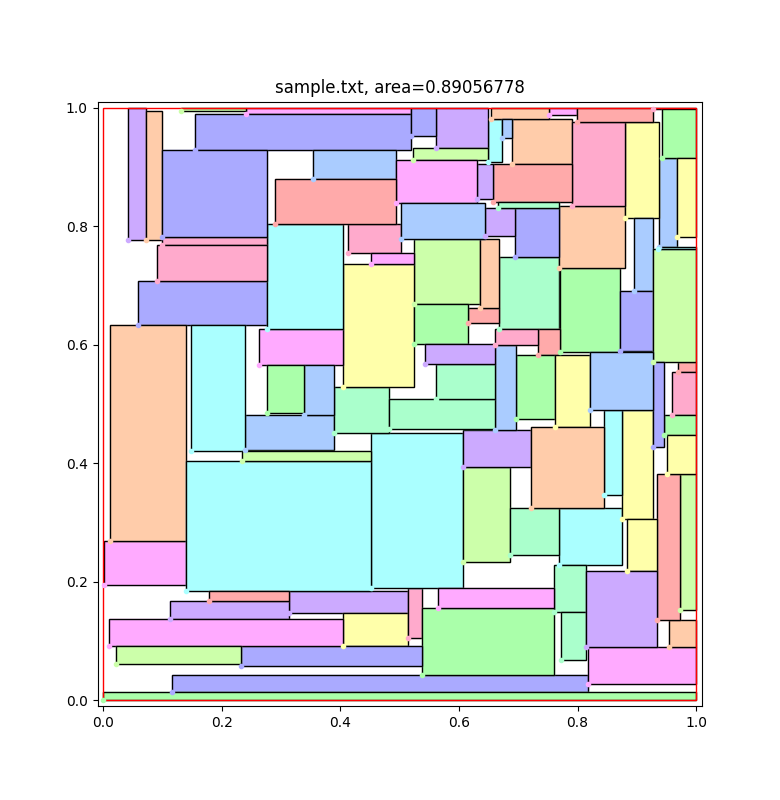
プログラム
アルゴリズム
各頂点の右方向のスピードと上方向のスピードを遺伝子として、 遺伝的アルゴリズムを実装した。
遺伝子から解を作成する
与えられた遺伝子から解を作成するアルゴリズムを解説する。
任意の 2 頂点の優先度を計算する
まず、2 頂点 $p_i, p_j$ に対する、最大の長方形を考える。
ここで、$p_i, p_j$ の位置関係を用いて場合分けを行う。
$p_j$ が $p_i$ の第 1 象限にある場合
$r_i$ が成長すると $p_j$ に衝突する。
$t_x \lt t_y$ の場合、$r_i$ は $p_j$ に下からぶつかる。
$t_y \lt t_x$ の場合、$r_i$ は $p_j$ に左からぶつかる。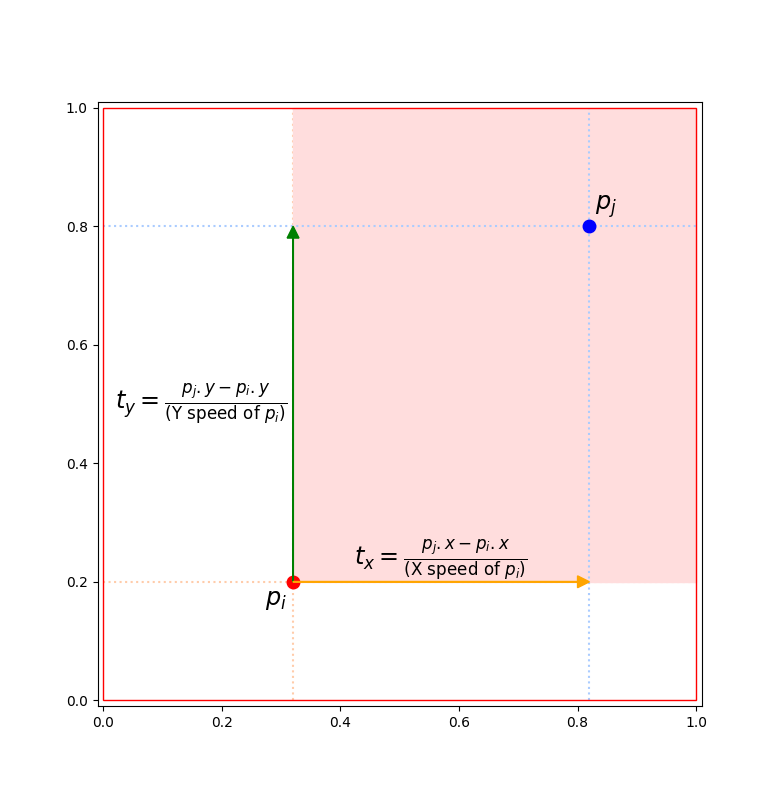
$p_j$ が $p_i$ の第 2 象限にある場合
$t_i \lt t_j$ の場合、$r_j$ は $r_i$ に左からぶつかる。
$t_j \lt t_i$ の場合、$r_i$ は $r_j$ に下からぶつかる。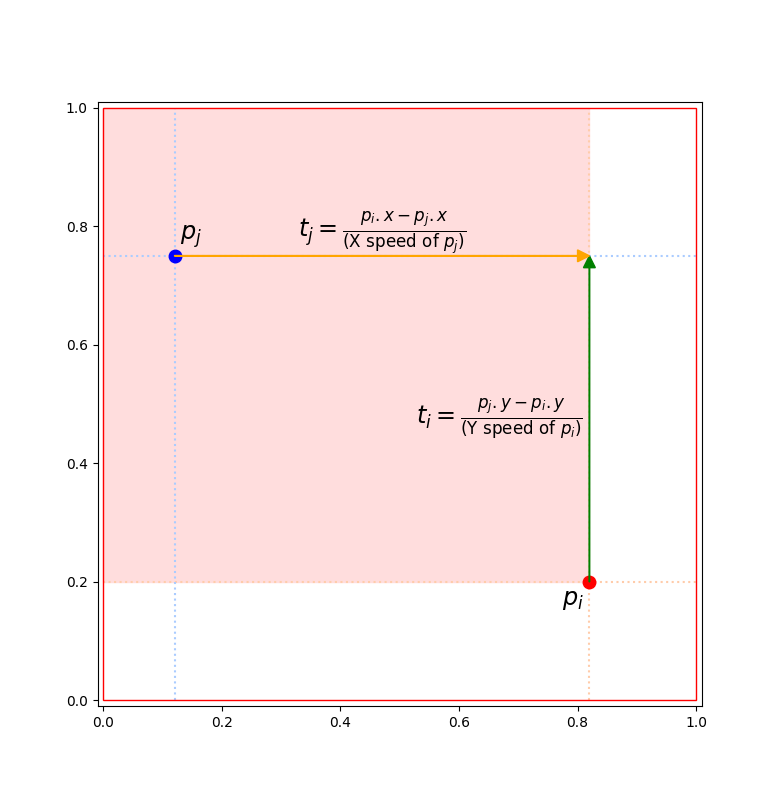
$p_j$ が $p_i$ の第 3 象限にある場合
$r_i$ が成長すると $p_j$ に衝突する。
$t_x \lt t_y$ の場合、$r_j$ は $p_i$ に下からぶつかる。
$t_y \lt t_x$ の場合、$r_j$ は $p_i$ に左からぶつかる。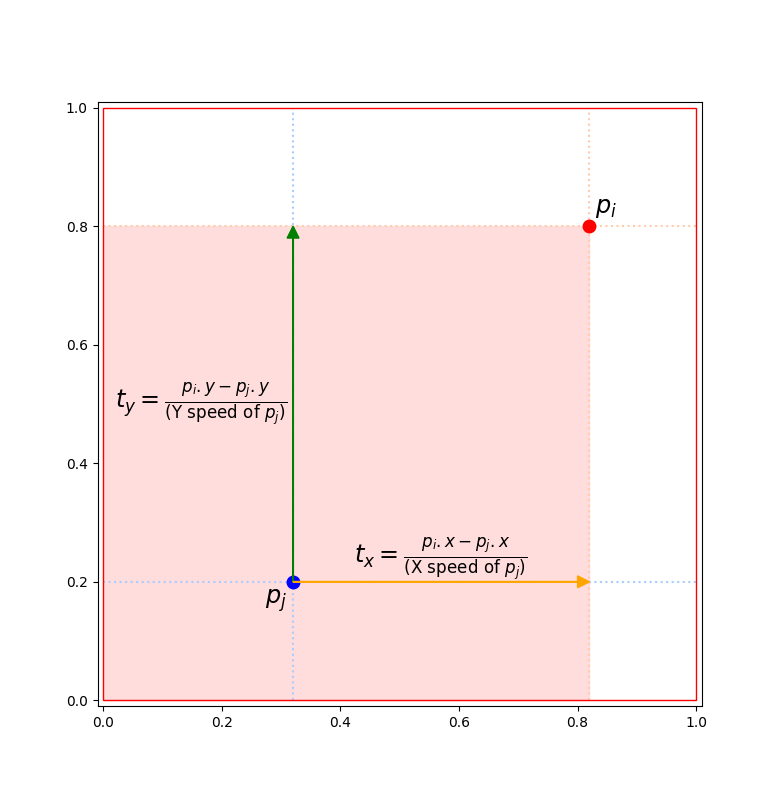
$p_j$ が $p_i$ の第 4 象限にある場合
$t_i \lt t_j$ の場合、$r_j$ は $r_i$ に下からぶつかる。
$t_j \lt t_i$ の場合、$r_i$ は $r_j$ に左からぶつかる。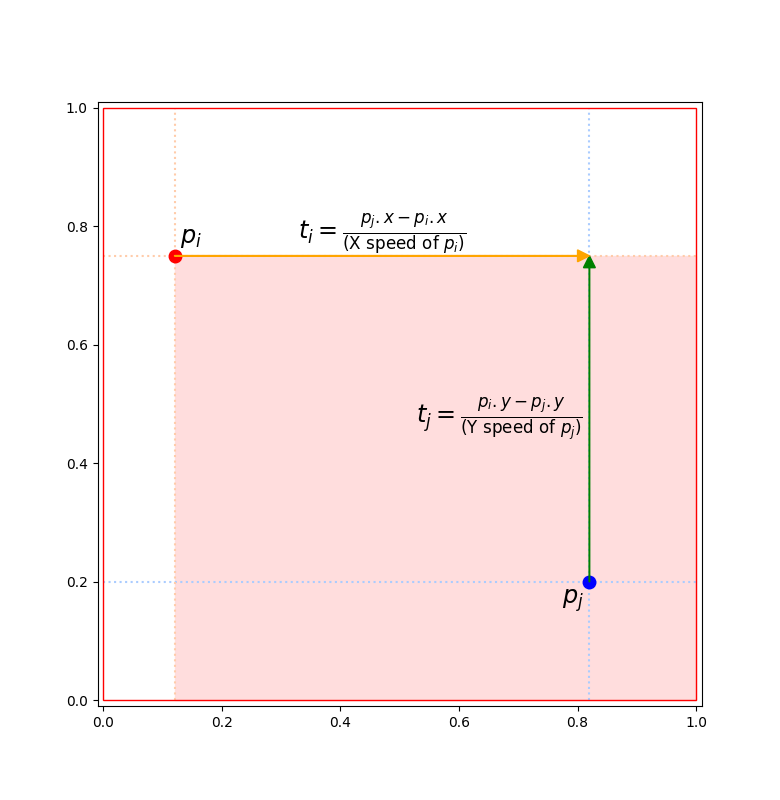
長方形 $r_i$ の配置
頂点 $p_i$ に長方形を配置する。
すべての長方形は $r_i = (x_i, y_i, x_i, y_i)$ で初期化しておく。
他の長方形 $r_j (j \ne i)$ と重ならなく、面積の大きい長方形を配置する。
これは $x_i^\prime = 1, y_i^\prime = 1$ として、$r_i$ と $r_j$ が重なったときに、
重ならなくなるまで $x_i^\prime, y_i^\prime$ を小さくすることで実現できる。
これだけでは、以下の画像の 3 番目の解が出力される。
3 番目の段階で最後に左から衝突しているので、最後に上方向に伸ばすことで面積を大きくすることができる。
遺伝子の交叉
遺伝的アルゴリズムにおける遺伝子の交叉を説明する。
今回実装したのは、1 世代に 100 個体、1000 世代の遺伝的アルゴリズムである。
各世代の 100 個体の中で、最も良い解を得られた 2 個体を親として、
次の世代の 100 個体を生成する。
ある遺伝子に注目すると、どちらかの親の遺伝子を 50%ずつの確率で受け継ぐ。
その後、5%の確率で突然変異する。突然変異ではランダムな値(スピード)を設定する。
最初の遺伝子は、乱数を用いて初期化する。