要約
パズルゲーム Katamino の解の数を数えるプログラムを作成した。
※ミノの複数形は minoes だが、プログラム等では minos と記載してしまっている。
プログラム
アルゴリズム
メインアイデア
全てのマスに番号を付け、1 つずつマスを埋めていく。
ここで、埋められないようなマスが存在するなら他の詰め込みを考える。
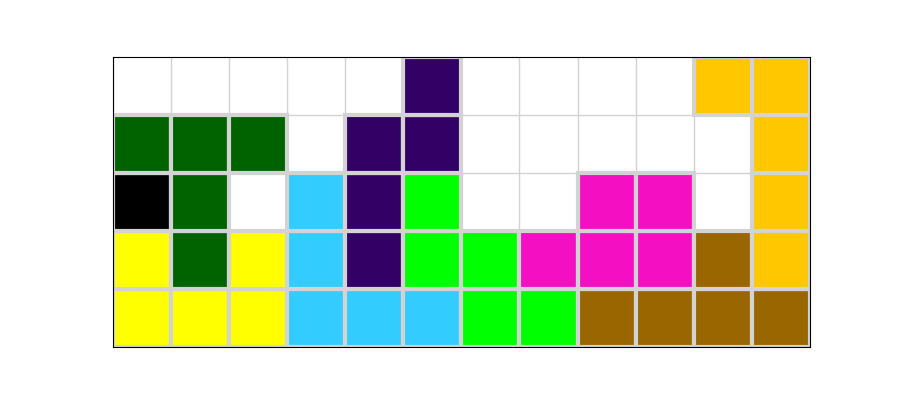
例えば、左下から右方向に詰め込みを行うと,
黒マスには残りのミノのどれもが配置できないため、ひとつ前に配置したミノを取り除いて再度詰め込みを行う。
 これは再帰を用いて効率的に書くことができる。
これは再帰を用いて効率的に書くことができる。
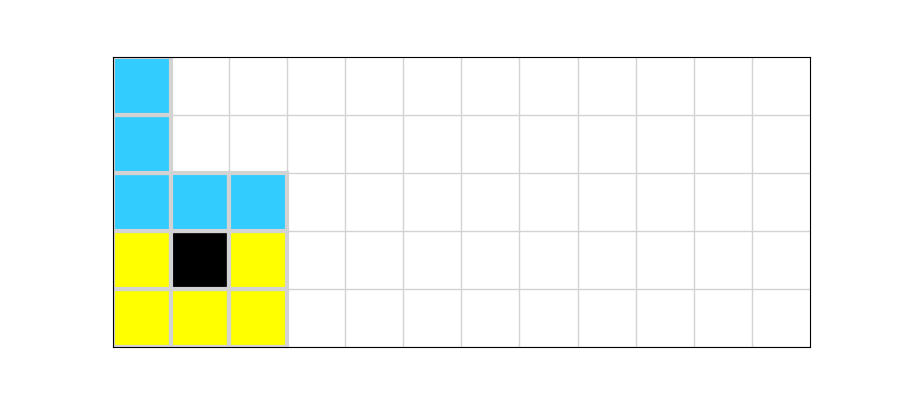
ここで、詰め込み方向は短辺方向が良い。
以下のように詰め込むと早い段階で詰め込みが出来なくなり、枝刈りの効率が良い。
X ミノを使用するときの重複排除(2D)
今回は、左右や上下を反転した解は重複した同じ解としてカウントする。
つまり全通りを探索すると、すべての解の 4 重複を計算することになる。
ここで、X ミノは反転しても形が変わらないことに注目すると、
X ミノの中心位置によって場合分けすることで効率的に計算することができる。
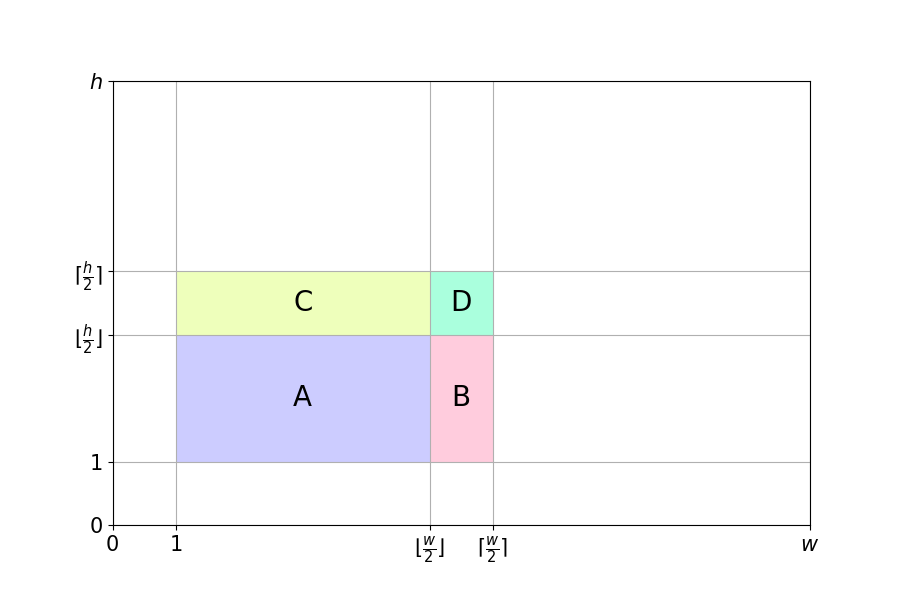
| X の中心位置 | 説明 |
|---|---|
| A | 重複する解は存在しない |
| B | 左右反転したものを重複して数える |
| C | 上下反転したものを重複して数える |
| D | 左右・上下反転したものを重複して数える |
このような場合分けを行うと、探索領域が 1/4 になり計算量が削減できる。
実行時間を比べると以下のようになる。
| サイズ | オリジナル | 重複排除後 |
|---|---|---|
| 10x6 | 16569ms | 1704ms |
| 12x5 | 5331ms | 665ms |
| 15x4 | 1080ms | 123ms |
| 20x3 | 61ms | 11ms |
OpenMP による高速化
各領域における処理を並列化することで、実行時間を短縮することができる。 実行時間を比べると以下のようになる。
| サイズ | 重複排除後 | 並列化後 |
|---|---|---|
| 10x6 | 1704ms | 1030ms |
| 12x5 | 665ms | 383ms |
| 15x4 | 123ms | 120ms |
| 20x3 | 11ms | 8ms |
3 次元への応用
基本的にはメインアイデアと同様である。
今回は実装を楽にするために、
あるマスにミノを配置するときに 2 次元詰込みのプログラムを再利用している。
あるマスにミノを配置するときには、
そのマスのある XY 平面、YZ 平面、ZX 平面にそれぞれ配置することで、
2D のコードを再利用できる。
ここで、I ミノは 1x1x5 なので、
1x1 で 90 度回転したものを重複して数えてしまう事に注意。
(実行結果を 1/2 にしなければならない。)
実行時間は 8,607,391ms(約 143 分) になる。
I ミノを使用するときの重複排除(3D)
2 次元の X ミノと同様に、3 次元では I ミノの位置で重複を排除できる。
I ミノは長さが 5 なので、3x4 平面に配置することはできない。
つまり、解を 3x4 平面で切ると、I ミノが 1 マス存在している。
3x4 平面上の I ミノの位置で場合分けを行う。
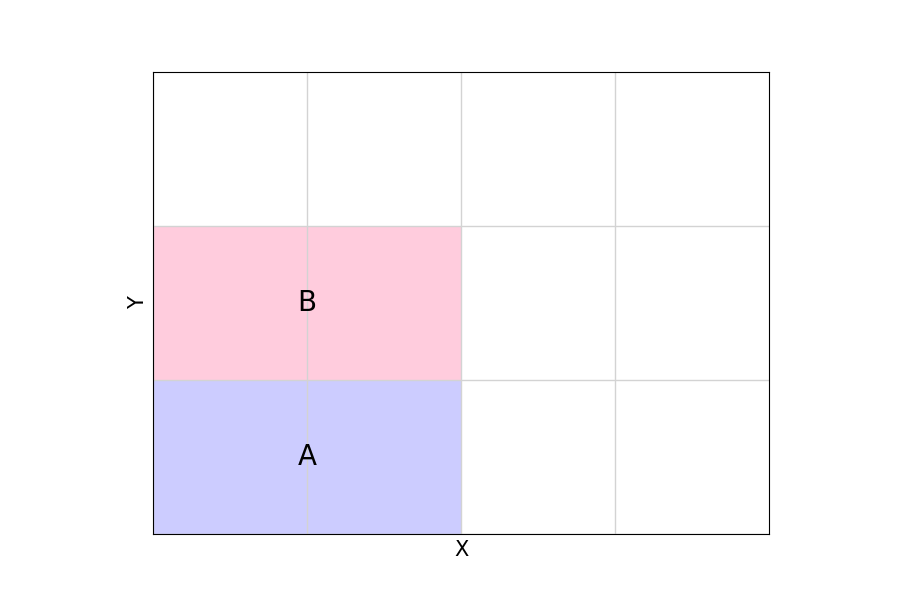
| I の中心位置 | 説明 |
|---|---|
| A | 奥行方向に反転したものを重複して数える |
| B | 奥行方向・上下反転したものを重複して数える |
以上の重複排除と OpenMP による高速化を行うと、
実行時間は 2,209,203ms(約 37 分) となり、非常に短縮できた。
実行結果
最終的な解の数をまとめると以下のようになる。
| サイズ | 10x6 | 12x5 | 15x4 | 20x3 | 11x5 | 10x5 | 9x5 |
|---|---|---|---|---|---|---|---|
| 種類数 | 2339 | 1010 | 368 | 2 | 4103 | 6951 | 5902 |
| サイズ | 8x5 | 7x5 | 6x5 | 5x5 | 4x5 | 3x5 | 3x4x5 |
|---|---|---|---|---|---|---|---|
| 種類数 | 3408 | 1396 | 541 | 214 | 50 | 7 | 3940 |