要約
RSA暗号の暗号化・復号化を計算するための電卓アプリ。 2つの素数を入力し、上段で暗号化、下段で復号化の演算を行っている。
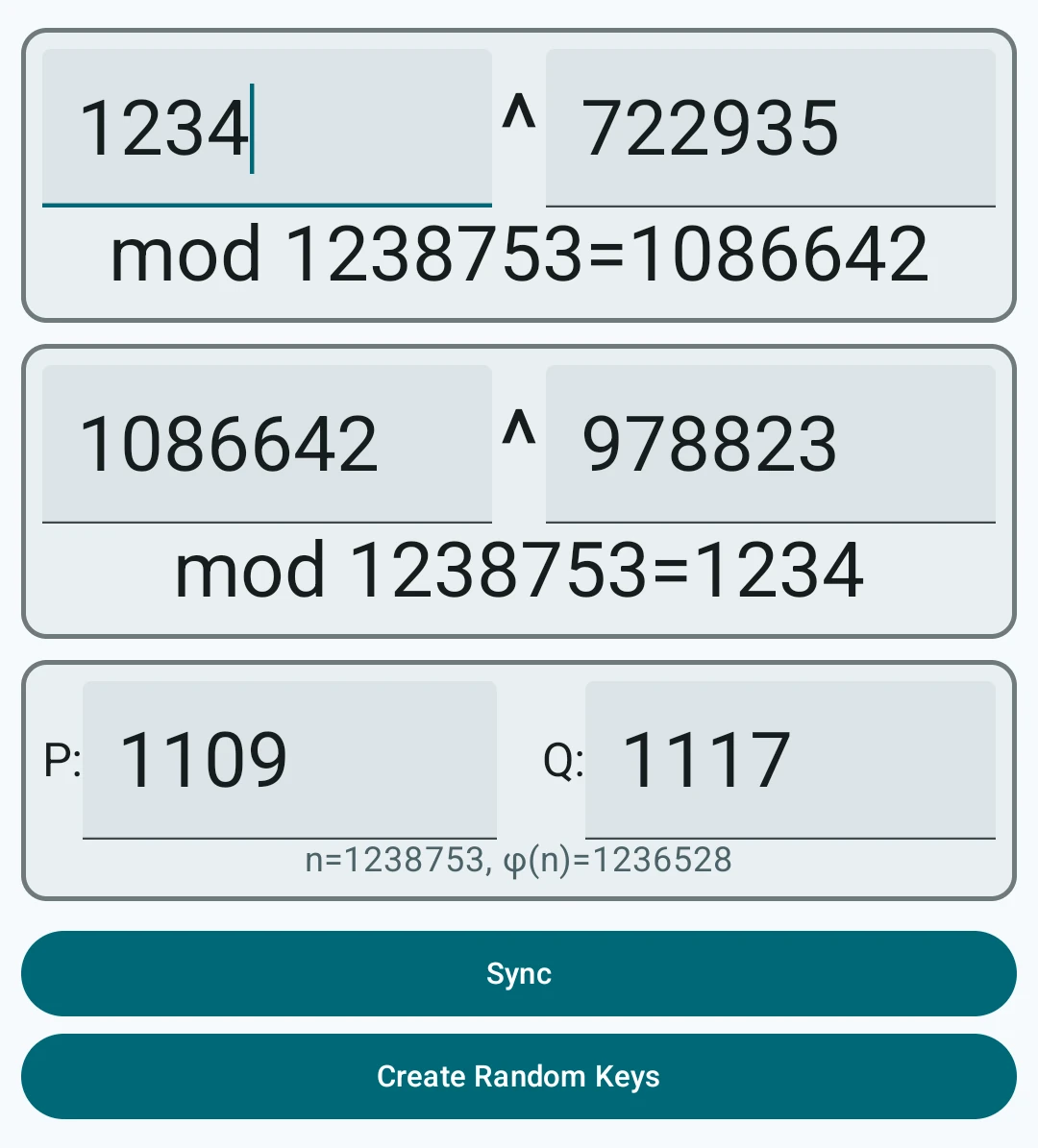
解説
鍵の生成
2つの素数 $p, q$、暗号化したい数値(平文) $m \notin \lbrace p, q \rbrace$ において、 $n$、$\phi(n)$1を定義する。
$$ n = p \cdot q $$ $$ \phi(n) = (p-1)(q-1) $$
$n, m$ は互いに素なのでオイラーの定理2より以下が成り立つ。 $$ m^{\phi(n)} \equiv 1 \quad(\bmod n)$$ $$ m^{\phi(n)+1} \equiv m \quad(\bmod n)$$
ここで、暗号化鍵(公開鍵) $d$、復号化鍵(秘密鍵) $e$ は以下のように表すことができ、 $d$ を決めると、拡張ユークリッドの互除法3を用いて $e$ を求められる。($d,e > 0$)
$$ d \cdot e \equiv 1 \quad (\bmod\ \phi(n)) $$
以上より、
- 公開鍵: $(d, n)$
- 秘密鍵: $(e, n)$
を求められた。
暗号化
平文 $m$ を、公開鍵を使って暗号化し、暗号文 $s$ を得る。 $$ s = m^d \mod n $$
復号化
暗号文 $s$ を、秘密鍵を使って複合化し、平文 $m$ を得る。 $$ m = s^e \mod n $$
復号できているか確認
$d \cdot e \equiv 1 \quad (\bmod\ \phi(n))$ より、 $d \cdot e = k\phi(n) + 1\quad (k\in \N)$と置く。
$$ s^e \equiv m^{d\cdot e} \equiv m^{k\phi(n)+1} \equiv m^{\phi(n)} \cdot m^{\phi(n)} \cdots m^{\phi(n)}\cdot m \equiv m\quad (\bmod n)$$
$m = s^e\mod n$ となり、復号できていることがわかる。
高速指数演算
$a^e\mod n$ の計算を高速に行う必要がある。
まず、$e$ を $m$ ビット整数と仮定し各桁を $b_i \in \lbrace 0, 1 \rbrace$ で表す。 $$ e = \sum_{i=0}^{m-1} b_i\cdot 2^i $$ $$ a^e = \prod_{i=0}^{m-1} a^{b_i 2^i} = \prod_{i=0}^{m-1} (a^{2^i})^{b_i}$$
ここで次の式が成り立つので、下位ビットから計算すると $ O(m) = O(\log n) $で計算することができる。 また、計算途中でも $\bmod n$ を取れるので、オーバーフローを防ぎながら計算できる。 $$ a^{2^{i+1}} = (a^{2^i})^2 \bmod n $$